2.2.4 Un approccio alternativo: il T-model

Dopo aver presentato modelli fondati sull'attualizzazione dei dividendi o su indicatori di mercato, verrà analizzata di seguito una tecnica di valutazione dei titoli azionari di maggiore concretezza ed aderenza alla realtà: il T-Model (35).

Il T-Model si basa su di un'equazione, volta a definire un tasso di rendimento atteso (total return, da cui deriva T-Model); per stimare tale rendimento il modello parte dall'equazione di Gordon-Shapiro, già vista nel paragrafo 2.2.2, a proposito del modello di attualizzazione dei dividendi in crescita costante:

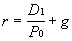
Il rendimento deriva dal tasso di dividendo (yield) e dal tasso di crescita (growth). Tale relazione può essere ulteriormente sviluppata, introducendo le determinanti del tasso di crescita, già viste in precedenza:

g = ROE (1 - b)

Fino ad ora si rimane nella logica dei modelli precedentemente sviluppati. A questo punto però il T-Model si contraddistingue per approfondire ulteriormente il significato del tasso di crescita aziendale; non si richiede la stima piuttosto arbitraria di payout o di tassi di crescita degli utili costanti all'infinito, ma ci si concentra molto più concretamente sulle relazioni tra crescita aziendale, necessità di adeguamento del patrimonio e conseguente ricorso ad operazioni di variazione del capitale sociale.

Le ipotesi del modello di Estep sono meno restrittive rispetto ai modelli precedenti. In primo luogo si assume che il risultato economico, il risultato operativo, la struttura finanziaria e il turnover delle attività totali rimangano costanti, il che può anche implicare che le grandezze in oggetto mutino dello stesso tasso percentuale.

In secondo luogo si ipotizza che il finanziamento della crescita avvenga attingendo innanzitutto agli utili non distribuiti e, nel caso fossero insufficienti, ad aumenti di capitale a pagamento, interpretati come una sorta di dividendo negativo; nel caso opposto di eccedenza dell'autofinanziamento rispetto alle esigenze di crescita patrimoniale , si genera un free cash flow destinato al riacquisto sul mercato di azioni proprie, che costituisce per i soci un rendimento aggiuntivo rispetto al normale dividendo. Le scelte in materia di distribuzione di dividendi diventano quindi ininfluenti per la formazione del rendimento atteso del titolo: gli azionisti percepiscono oppure pagano una somma pari alla differenza tra utili netti e variazione del patrimonio determinata dalla crescita aziendale.

Rappresentiamo in questo modo la prima parte dell'equazione del rendimento atteso, corrispondente al cosiddetto cash flow yield:

La variabile Xcf corrisponde all'excess cash flow destinato, come si diceva, al riacquisto sul mercato di azioni proprie nel caso sia positivo e all'emissione di nuove azioni nel caso sia negativo. L'excess cash flow si ottiene chiaramente sottraendo agli utili netti non distribuiti, il fabbisogno determinato dal finanziamento della crescita (tasso di crescita g moltiplicato per l'ammontare del patrimonio iniziale Pn):

Sostituendo questa definizione nella formula del cash flow yield, si ottiene:

da cui, dividendo numeratore e denominatore per Pn0 (essendo la redditività del capitale proprio Roe pari all'utile diviso per il patrimonio netto) si avrà:

Rimane ora da determinare una seconda componente del rendimento atteso, quella crescita in linea capitale che corrisponde alla variazione percentuale del prezzo di mercato. Il controvalore delle azioni, in termini di patrimonio netto contabile, sarà variato rispetto all'ammontare iniziale in ragione del tasso di crescita g. Di conseguenza la variazione percentuale di prezzo potrà essere spiegata dalla trasformazione in valori di mercato dei valori netti contabili, attraverso il multiplo Prezzo/Patrimonio netto; perciò la componente di rendimento in linea capitale sarà determinata sia dal tasso di variazione contabile del patrimonio g e sia dalla modificazione del multiplo Prezzo/Patrimonio netto. Riassumendo in termini algebrici:

Per cui sommando le due componenti del cash flow yield e della variazione percentuale di prezzo, si ottiene il rendimento complessivo atteso T del modello di Estep definito secondo la seguente equazione:

Dall'equazione finale del modello si evince che la previsione dei rendimenti attesi implica la stima del tasso di crescita del patrimonio, del Roe e della variazione del multiplo P/Pn. Rispetto ad altri modelli quindi il T-model ha il pregio di considerare prevalentemente grandezze contabili; la stima del Roe si riduce alla previsione dell'utile netto, con gli accorgimenti indicati in precedenza nell'ambito del metodo di mercato; anche per la stima del tasso di crescita g ci si può riferire a quanto enunciato nell'ambito dei modelli di attualizzazione dei dividendi. Il problema principale della stima del rapporto P/Pn viene aggirato ipotizzando che tenda a convergere gradualmente verso un valore medio-normale di settore; questa forzatura non inficia la bontà del modello, in quanto in alcune verifiche empiriche (36) effettuate sul mercato americano si è riscontrato che la maggior parte dei rendimenti medi realizzati, è spiegata dalla somma dei primi due termini, che presentano tra l'altro anche una variabilità minore.

Le stesse verifiche effettuate sembrerebbero dimostrare che i portafogli composti da azioni selezionate in base all'elevato rendimento atteso stimato dal T-model, ottengono ottime performance rispetto all'indice di mercato, con una volatilità di poco superiore. Ma ci sono altri buoni motivi per utilizzare il modello di Estep nella valutazione dei titoli azionari: maggiore concretezza, variabili direttamente desumibili da fonti correntemente utilizzate dagli analisti, rendimenti di periodo a breve termine ed approccio equilibrato.