CAPITOLO 4 - L'EFFICIENZA DEI MERCATI
4.2.1 Il Random walk
Nelle prime formalizzazioni del modello del mercato efficiente, il prezzo che
riflette pienamente tutte le informazioni veniva interpretato nel senso che
le successive variazioni dei prezzi erano indipendenti.
Inoltre veniva usualmente ipotizzato che le successive variazioni dei prezzi
fossero identicamente distribuite.
Le due ipotesi congiunte costituiscono il famoso modello di random walk
(cammino casuale) 1.
In termini formali:
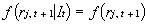
L'ipotesi è che le distribuzioni di probabilità condizionate e
marginali di una variabile casuale indipendente sono tra loro identiche ed
inoltre si assume che la funzione di densità f sia la stessa
per ogni t.
In realtà si deve notare come nella letteratura sul random walk
si assuma solitamente che l'insieme delle informazioni It
includa solo la storia dei rendimenti passati; di conseguenza la verifica
empirica del modello costituisce un modo per sperimentare l'efficienza in
forma debole del mercato finanziario.
D'altro canto il modello del random walk è certamente un'ipotesi
più restrittiva rispetto all'ipotesi iniziale dell'efficienza
informativa, per cui la sua validità è condizione sufficiente
ma non necessaria perché si possa parlare di efficienza debole; infatti
mentre quest'ultima asserisce che il valore atteso della distribuzione dei
rendimenti è indipendente dalle informazioni It ,
la passeggiata a caso esige in più che l'intera distribuzione,
e non solo la media, sia indipendente da It .
Certamente tale distinzione non è stata subito chiara; alcune imprecisioni
degli studi iniziali sul random walk sono comunque comprensibili, se si
considera che la ricerca non è partita dallo sviluppo di una teoria di
determinazione dei prezzi, bensì dall'accumulazione, tra la metà
degli anni '50 e i primi anni '60, delle prove che l'andamento dei prezzi azionari
erano ben approssimabili da un random walk.
Nel 1953, nell'ambito di uno studio sul comportamento settimanale di diciannove
indici azionari britannici, nonché dei prezzi a pronti di cotone e grano,
Kendall affermò:
"La serie sembra girovagare, quasi come se ogni settimana il caso estraesse da
una popolazione simmetrica con distribuzione fissa un numero casuale, e lo
aggiungesse al prezzo corrente per determinare il prezzo della settimana successiva".
Quasi dieci anni dopo Cootner 2, in un celebre lavoro
in materia, tentava di fornire le prime spiegazioni al modello della passeggiata a caso,
tentando di caratterizzare l'ambiente in cui si sviluppa:
"Se un gruppo consistente di compratori pensasse che il prezzo è troppo
basso, i loro acquisti farebbero salire il prezzo; il contrario avverrebbe per i
venditori.
... l'aspettativa condizionata del prezzo di domani, dato il prezzo di oggi, è
il prezzo di oggi.
In tale mondo le sole variazioni di prezzo che si possono verificare derivano da nuove
informazioni.
Siccome non c'è alcun motivo per ritenere che si presentino in forma non
casuale, le variazioni dei prezzi azionari di periodo in periodo dovrebbero essere
casuali e indipendenti tra loro."
Solo con i modelli di Samuelson e di Mandelbrot 3
si perviene però ad una formulazione più rigorosa dei modelli di
gioco equo e dei loro collegamenti con la teoria del random walk.
In base alle loro analisi sui contratti futures dei mercati delle merci,
essi mostrarono che il prezzo di un tale contratto al tempo t era il
valore atteso in t del prezzo spot alla scadenza del contratto; allora
il prezzo future segue una martingala rispetto alla successione
delle informazioni, cioè la variazione attesa del prezzo da periodo a
periodo è nulla e quindi segue un gioco equo.
1 L'esempio classico è quello del modo di camminare di un ubriaco, che è del tutto imprevedibile; pertanto la posizione dell'ubriaco al tempo t+1 ha come valore atteso, cioè come posizione pi� probabile, il punto noto in cui si trovava al tempo t. Non esiste la possibilità di utilizzare altre informazioni sulle posizioni precedenti per migliorare le previsioni circa la posizione futura.
2 Cootner P., The Random Character of Stock Market Prices, Cambridge, MIT Press (1964).
3 Samuelson P.A. Proof That Properly Anticipated Prices Fluctuate Randomly, Industrial Management Review (1965);
Mandelbrot B. The Variation of Some Other Speculative Prices, Journal of Business (1967).